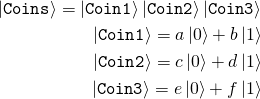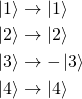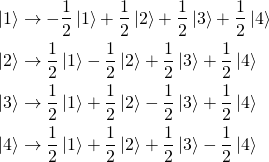Немного о квантовых компьютерах

21 декабря 2018 года Дональд Трамп подписал «National Quantum Initiative (NQI) Act», которым предусматривается выделение в течение следующих пяти лет 1,2 млрд долларов на исследования в области квантовых компьютеров. Деньги немалые, и возможно кому-то из читателей ПиМ станет интересно, куда пойдут деньги американских налогоплательщиков. Сейчас в интернете очень много научно-популярных материалов о том, что такое квантовый компьютер и зачем он нужен, и тем не менее, я решил написать ещё один.
Основную проблему научно-популярных текстов и видео можно описать этим диалогом из «Симпсонов» (Дом Ужасов 6):
Профессор Фринк: Вот обычный квадрат... [рисует на доске квадрат]
Шеф Виггам: Воу! Воу! Давай что-то попроще!

Для многих простота изложения — это отсутствие в нём математических формул. При этом наверняка есть и другие люди, которые, с одной стороны, не против пощупать математику, которая стоит за словами и метафорами научно-популярных текстов. Но с другой стороны, если брать профессиональную книгу, то в ней можно заблудиться в детялях, так и не дойдя до сути. Этот текст я пишу в расчёте на читателя из второй категории, который не боится некоторого количества чисел и математических значков в тексте.
Итак, в чём же недостаток обычных компьютеров и зачем нам нужны ещё какие-то особенные квантовые компьютеры? Причина состоит в том, что даже очень, казалось бы, простую квантовую систему невозможно промоделировать на обычном компьютере. Представим себе для начала обычную «классическую» частицу («классический» тут означает «не квантовый»). Самая простая для описания вещь — это «монетка», которая имеет всего два возможных состояния «орёл» и «решка». Не нужно снисходительно относиться к монетке как к примеру, ибо даже Леонард Сасскинд рассказывает о важности симметрий в физике на примере монеток и смены состояния Орёл-Решка (Heads-Tails):

Допустим, нам неинтересно, что происходит с монеткой, когда состояние меняется, как она переворачивается, крутится… такая небрежность допустима, например, если большую часть времени с монеткой ничего не происходит и только изредка она мгновенно переворачивается. Для описания состояния такой монетки ( ![]() ) нам нужен всего один бит информации — «0» или «1» («орёл» или «решка»).
) нам нужен всего один бит информации — «0» или «1» («орёл» или «решка»).
![]() — монетка находится в состоянии «орёл»
— монетка находится в состоянии «орёл»
![]() — монетка находится в состоянии «решка»
— монетка находится в состоянии «решка»
Всё просто. Допустим, что у нас теперь система из трёх таких монеток. Сколько нужно компьютерной памяти для описания состояния такой системы? — Очевидно, что три бита. Например, состояние
означает «первая монетка в состоянии «орёл», а вторая и третья — «решки». Если у нас N таких монеток, то нам нужно N бит компьютерной памяти, чтобы полностью описать состояние этих N монеток. Современный ноутбук или смартфон без проблем может хранить состояние системы из миллионов таких монеток. Теперь возьмем квантовую монетку. Состояние одной квантовой монетки, на которую ещё не посмотрели, описывается не битом, а двумя числами a и b:
Важно знать, что нет и не может быть никакого устройства, прибора, в который можно было бы положить эту квантовую монетку и он бы выдал значения a и b. Вообще-то, a и b— комплексные числа, но для понимания сути проблемы можно представить, что это обычные числа в промежутке от -1 до 1. Причём, a2— это вероятность увидеть монетку в состоянии «орёл», когда на неё посмотреть, а b2 — вероятность увидеть «решку». Очевидно, что a2+b2=1. Например:
Если бы в формуле выше вместо знака «-» стоял бы «+», то вероятности увидеть «орёл» или «решку» не изменились бы, но тем не менее, это было бы другое состояние квантовой монетки! Итак, иметь наиболее полную информацию о состоянии монетки — это знать два числа a и b. При этом, однако, мы не знаем — увидим ли мы монетку в состоянии «орёл»или в состоянии «решка», когда на неё посмотрим. Важный момент: максимальная полнота знания о состоянии ещё не гарантирует отсутствие случайностей при последующем измерении. Но зато если мы посмотрели на монетку и увидели её в состоянии, например, «решка» — это значит, что тем самым мы изменили числа a и b таким образом, что теперь a=0 и b=1.Это значит, что если мы опять посмотрим на монетку, на которую только что смотрели, то всё — никаких случайностей не будет, в 100% случаев монетка будет в состоянии «решка».
В связи с популярностью мемов, связанных с котом Шрёдингера, и непониманием того, что не всякие вероятности и неопределённости — квантовые, нужно сделать крайне важное замечание. Пусть есть монетка, но она «закрыта в ящике», и мы ещё на неё не смотрели. Тогда можно описать две ситуации, в которых есть незнание и вероятности:
1) Я знаю, что монетка находится или в состоянии «орёл» ![]() или в состоянии «решка»
или в состоянии «решка» ![]() , причём, с вероятностью 2/3 — монетка в закрытом ящике находится в состоянии «решка» (
, причём, с вероятностью 2/3 — монетка в закрытом ящике находится в состоянии «решка» ( ![]() )
)
2) Я знаю, что монетка в закрытом ящике точно находится в состоянии ![]() , и поэтому вероятность обнаружить монетку в состоянии «решка»равна 2/3.
, и поэтому вероятность обнаружить монетку в состоянии «решка»равна 2/3.
Так вот — это две разных ситуации и два разных утверждения! В первом случае наше знание о состоянии монетки меньше, чем во втором случае. В первом случае мы не уверены не только в том, в каком состоянии мы увидим монетку, но мы даже не уверены в том, какое её состояние сейчас, до того, как мы на неё посмотрим. Во втором случае мы точно знаем состояние монетки до того, как на неё смотреть. При этомнаши априорные знания о вероятностях обнаружить монетку в состоянии «решка» — одинаковые в обоих случаях. Первый случай соответствует классической монетке, которую каким-то образом кто-то положил в ящик. Она определённо лежит в ящике или орлом или решкой, но мы просто не знаем, как именно, пока не посмотрим. Можно сказать, что энтропия монетки в первом случае не нулевая, а во втором случае нулевая (энтропия — это не только степень беспорядка, но ещё уровень незнания).
Возвращаясь к трудностям. Мы видим, что вместо одного бита для описания монетки теперь нужно два числа типа float. Но главные проблемы начинаются при добавлении других квантовых монеток в систему. Пусть у нас есть три квантовых монетки, сколько же чисел нам нужно, чтобы описать их состояние? Можно было бы подумать, что нужно 2х3=6 чисел a, b, c, d, e, f:
Это было бы верно, если бы монетки не «чувствовали» бы друг друга — такие совершенно независимые, отдельные монетки. Но в общем случае состояние трёх квантовых монеток должно описываться восемью числами a, b, c, d, e, f, g, h:
Ведь смотрите, при измерении состояния трёх монеток мы можем получить восемь вариантов: все три «орлы», первые две «орлы», а третья «решка, … и т. д., вплоть до все три «решки». И (главное правило квантового мира!) для каждого варианта должно быть своё число! И квадрат этого числа равен вероятности обнаружить три монетки именно в такой конфигурации. То есть, если мы хотим использовать компьютер для описания состояния N квантовых монеток, то нам нужно хранить примерно 2N (два в степени N) чисел в памяти компьютера. Когда N=10, то всё вполне просто — подумаешь, всего тысяча чисел. Но если у нас 100 квантовых монеток, то тогда нам нужно иметь компьютер с примерно 1022(десять в 22 степени) гигабайт памяти. И это только лишь для того, чтобы хранить состояние. Но для вычислений нам же нужно работать с квадратными матрицами таких размеров, перемножать и складывать все эти 2100 чисел. Так что, выложенные в квадрат десять на десять квантовые монетки — это уже неподъёмная задача для всех компьютеров планеты. А что же тогда говорить про моделирование сложных атомов, молекул или вещества, где может быть тоже сотни квантовых ядер, электронов… и в отличие от наших «простых» монеток у них может быть у каждого не два состояния «орёл» и «решка», а намного больше.

Решение проблемы : моделировать квантовые системы нужно на квантовых же компьютерах!
(Фейнман, 1982)
Квантовый компьютер с одной стороны — это квантовая система, как наши квантовые монетки, которые вообще-то называются кубитами. Кубит (qubit, квантовый бит) — это и есть описанная выше «монетка», которая имеет два разных состояния: «орёл» и «решка», «левый» и «правый» ![]()
![]() , «горизонтальный» и «вертикальный»
, «горизонтальный» и «вертикальный» ![]()
![]() , «вверх» и «вниз»
, «вверх» и «вниз» ![]()
![]() , «ground» and «excited»
, «ground» and «excited» ![]()
![]() , «живой» и «мертвый»
, «живой» и «мертвый» ![]()
![]() (если речь о коте Шрёдингера) и т.д. Результат работы квантового компьютера не может быть рассчитан на обычном компьютере, выше я показал почему. Но с другой стороны, квантовый компьютер — это система, которую можно настраивать, система, которой можно управлять. Например, если квантовый компьютер — это те самые 100 квантовых монеток-кубитов, то мы должны уметь физически приготавливать исходные состояния перед вычислением (например — приготовить все кубиты в состоянии «орёл»). И что самое важное, управлять тем, как кубиты друг с другом взаимодействуют. Совсем абстрактно, представьте, что сначала мы приготовили 100 кубитов по отдельности в состоянии «орёл», и эти кубиты «лежат» не рядом, они «друг друга не чувствуют», а потом мы «берём» кубит номер 37 (не глядя на него, и не измеряя его состояние!) и подносим к кубиту номер 63, даём им провзаимодействовать, и потом разносим их (опять-таки, не измеряя результат!)Потом кубит номер 63 (состояние которого после взаимодействия стало неопределённым) подносим к кубиту номер 18…и так далее. Такжемы можем не «подносить» кубиты друг к другу, а «переворачивать» монетки-кубиты по отдельности (опять же, не измеряя результат!) Например, простейшая операция с квантовой монеткой выглядит так:
(если речь о коте Шрёдингера) и т.д. Результат работы квантового компьютера не может быть рассчитан на обычном компьютере, выше я показал почему. Но с другой стороны, квантовый компьютер — это система, которую можно настраивать, система, которой можно управлять. Например, если квантовый компьютер — это те самые 100 квантовых монеток-кубитов, то мы должны уметь физически приготавливать исходные состояния перед вычислением (например — приготовить все кубиты в состоянии «орёл»). И что самое важное, управлять тем, как кубиты друг с другом взаимодействуют. Совсем абстрактно, представьте, что сначала мы приготовили 100 кубитов по отдельности в состоянии «орёл», и эти кубиты «лежат» не рядом, они «друг друга не чувствуют», а потом мы «берём» кубит номер 37 (не глядя на него, и не измеряя его состояние!) и подносим к кубиту номер 63, даём им провзаимодействовать, и потом разносим их (опять-таки, не измеряя результат!)Потом кубит номер 63 (состояние которого после взаимодействия стало неопределённым) подносим к кубиту номер 18…и так далее. Такжемы можем не «подносить» кубиты друг к другу, а «переворачивать» монетки-кубиты по отдельности (опять же, не измеряя результат!) Например, простейшая операция с квантовой монеткой выглядит так:
Никак не измеряя и не зная чему равны a и b, мы «переворачиваем» монетку:
И так далее (можно «переворачивать» не полностью, тогда будут задействованы синусы/косинусы в конечном результате).
И вот если вначале общее состояние набора кубитов было простым и могло описываться даже одной фразой «каждый кубит находится в состоянии «орёл», то после таких операций общее состояние уже становится крайне сложным для хранения на обычном компьютере. Это и есть вычисления, а «квантовая программа» и «входные данные» — это то, в каком порядке и что именно мы делаем с кубитами.
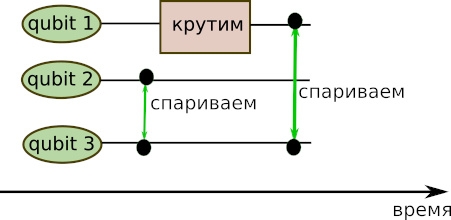
Конечный этап работы квантового компьютера — наконец-то посмотреть, в каком состоянии находится каждый кубит. Это и будет ответ, «результат вычислений». Конечно, в реальном квантовом компьютере кубиты друг к другу не подносят в руках, они зафиксированы в пространстве, но начинают взаимодействовать друг с другом, например, если на них светят лазером с определёнными параметрами.
Кубитыв повседневной жизни — это фотоны (частицы света), «орёл» и «решка» при этом — вертикальная ![]() или горизонтальная
или горизонтальная ![]() поляризация этих фотонов, а «измерительный прибор» (он же и прибор для приготовления фотонов в заданном состоянии) — это известный фотографам поляризатор. Поляризационные очки в кинотеатре IMAX сделаны так, что левый глаз зрителя получает фотоны
поляризация этих фотонов, а «измерительный прибор» (он же и прибор для приготовления фотонов в заданном состоянии) — это известный фотографам поляризатор. Поляризационные очки в кинотеатре IMAX сделаны так, что левый глаз зрителя получает фотоны ![]() , а правый глаз получает фотоны
, а правый глаз получает фотоны ![]() . Простейший эксперимент для любознательных: наденьте очки в IMAX и закройте один глаз, посмотрите на человека в таких же очках, потом посмотрите другим глазом. Попробуйте наклонить при этом голову на бок. Фотоны были бы отличными кандидатами на роль кубитов для квантового компьютера, их можно отлично вращать и измерять по отдельности, но, к сожалению, друг друга они практически не чувствуют.
. Простейший эксперимент для любознательных: наденьте очки в IMAX и закройте один глаз, посмотрите на человека в таких же очках, потом посмотрите другим глазом. Попробуйте наклонить при этом голову на бок. Фотоны были бы отличными кандидатами на роль кубитов для квантового компьютера, их можно отлично вращать и измерять по отдельности, но, к сожалению, друг друга они практически не чувствуют.
Приведённая выше схема универсального квантового компьютера была придумана Дэвидом Дойчем в 1989 году (кстати, рекомендую к прочтению его книги «Структура реальности» и «Начало бесконечности»).

Работающий квантовый компьютер IBM-Q (с пятью кубитами), доступен каждому через интернет, достаточно зайти на сайт проекта и зарегистрироваться.
Конечно, 5 кубитов элементарно моделируются на любом ноутбуке, но важен сам принцип… И этот сервис люди смело используют для того, чтобы добавить в свои статьи по квантовой информатике слова про «экспериментально подтверждено». Также этот сервис будет хорошей основой для лабораторных работ по квантовой механике в школах и университетах.
Теперь нужно ответить на вопрос: а что же такого может посчитать квантовый компьютер? И как вообще его программировать? К сожалению, писать квантовые алгоритмы непросто. Более того, неискушённому человеку может показаться, что задачи, для которых всё-таки придуманы квантовые алгоритмы, какие-то «искусственные», как будто люди специально придумали именно такие странные формулировки того, что нам дано и что мы хотим получить. Поскольку все часто говорят про алгоритм Шора, который «взломает интернет и банковскую тайну», при этом не вдаваясь в сложные детали, то здесь я лучше опишу другой, более наглядный квантовый алгоритм — алгоритм поиска, который придумал Лов Кумар Гровер в 1996 году.
Алгоритм Гровера. Представьте, что у вас имеется N штук пронумерованных закрытых коробок. Они все пустые кроме одной, в которой находится мячик. Ваша задача: узнать номер коробки, в которой находится мячик (этот неизвестный номер часто обозначают буквой w).
Пока что это обычные коробки и обычный мячик, ничего квантового. Как решать эту задачу? Самым тупым способом, по очереди открывать коробки, и рано или поздно вы наткнётесь на коробку с мячиком. А сколько в среднем коробок нужно проверить до того, как будет обнаружена коробка с мячиком? Наверное, даже не знакомому с математикой человеку интуитивно понятно, что может быть ситуация, когда «повезло» и мячик нашёлся сразу в первой открытой коробке, но может быть и ситуация «очень не повезло», когда пришлось открыть все коробки и мячик оказался в последней. Ну значит, в среднем нужно открыть примерно половину коробок N/2. Главное здесь то, что если мы увеличим число коробок в 100 раз, то в те же 100 раз увеличится и среднее число коробок, которые нужно открыть до того, как будет найдена коробка с мячиком. Пока что всёдовольно банально.
Теперь сделаем ещёодно уточнение. Пусть мы не сами открываем коробки руками и проверяем наличие мячика в каждой, а имеется некий посредник, назовем его Оракул (Oracle). Мы говорим Оракулу — «проверь коробку номер 732», и Оракул честно проверяет и отвечает «в коробке номер 732 мячика нет». Теперьвместо слов о том, сколько коробок нам нужно в среднем открыть, мы говорим «сколько раз в среднем мы должны обратиться к Оракулу для того, чтобы найти номер коробки с мячиком» (вы же понимаете, что нам важен не мячик, а номер коробки с мячиком?)
Итак, теперь мы готовы обсуждать квантовый алгоритм поиска. Оказывается, что если перевести эту задачу с коробками, мячиком и Оракулом на квантовый язык, то выходит замечательный результат: для поиска номера коробки с мячиком среди Nкоробок нам нужно потревожить Оракула всего примерно ![]() раз! Иначе говоря, если у нас миллион коробок, то нужно не 500 тысяч раз спрашивать Оракула, а всего тысячу. И если число коробок увеличивается в 100 раз, то число необходимых обращений к Оракулу возрастает всего в 10 раз. Однако, Оракул должен при этом быть квантовым, и мы должны уточнить, что конкретно означают слова «одно обращение к Оракулу».
раз! Иначе говоря, если у нас миллион коробок, то нужно не 500 тысяч раз спрашивать Оракула, а всего тысячу. И если число коробок увеличивается в 100 раз, то число необходимых обращений к Оракулу возрастает всего в 10 раз. Однако, Оракул должен при этом быть квантовым, и мы должны уточнить, что конкретно означают слова «одно обращение к Оракулу».
Для начала опять таки вернёмся к НЕквантовому Оракулу: что же это такое? Как можно себе это представить? Представим Оракул в виде «микросхемы», где есть Nвходов и Nвыходов. Внутри эта микросхема устроена просто: все провода проходят насквозь,и только провод, номер которого отвечает номеру «коробки с мячиком»,внутри микросхемы обрывается. Провода у нас идеальные, никакого сопротивления, шумов нет. Так что «обращением к Оракулу» будем считать прохождение одного электрона через схему по какому-то проводу. Если мы на выходе поймали электрон — значит «Оракул сказал, что это не тот номер». Если же мы запустили электрон по тому проводу, который оборван, то на выходе мы его не увидели, и для нас это знак того, что это и есть «тот самый провод», номер которого отвечает «той самой коробке с мячиком».

И главное: «обращение к Оракулу» — это «прохождение ОДНОГО электрона через устройство Оракула». Например, если мы запустим одновременно Nэлектронов по всем входам, то это будет не одно, а Nобращений к Оракулу. Вот такие правила.
А что же будет в квантовом случае? Мы по-прежнему запускаем один электрон, однако, он может находиться на всех проводах одновременно. В случае монетки у нас были состояния «орел» и «решка», а теперь в случае электрона у него есть состояния «на проводе номер 1», «на проводе номер 2»… «на проводе номер N». В дальнейшем остановимся на случае N=4 (это особый примечательный случай) и для примера помеченный провод будет номер 3. То есть, состояние одного запущенного электрона в общем случае будет задаваться четырьмя числами:
Квантовый Оракул каким-то образом должен выделять одно, «помеченное» состояние, один провод. И тут уже нельзя использовать банальный обрыв провода (ибо тогда квантовая магия исчезнет), электрон обязательно должен пройти через Оракула. Мы полностью зададим поведение Оракула, если укажем, как он будет изменять состояние электрона, который изначально был локализован на каждом проводе. И сделаем мы это таким образом:
Состояние электрона до попадания в Оракул → Состояние электрона после прохождения Оракула
Дело в том, что если у нас электрон находится весь на одном проводе, например, на втором, то состояния ![]() и
и ![]() — не различимы, физически это одно и то же состояние электрона. Нет и не может быть такого прибора, который бы заметил этот минус. Однако, если же мы подаём на Оракул «размазанный» по всем проводам электрон, то состояние трансформируется вот так:
— не различимы, физически это одно и то же состояние электрона. Нет и не может быть такого прибора, который бы заметил этот минус. Однако, если же мы подаём на Оракул «размазанный» по всем проводам электрон, то состояние трансформируется вот так:
И вот здесь этот минус уже играет роль, ибо состояние реально поменялось.
Но одного Оракула для удачной реализации поиска нам не хватит. Нужно ещёодно устройство с Nвходами и Nвыходами, через которое проходит размазанный электрон, после чего его состояние тоже как-то меняется. Однако, это устройство — не Оракул, и это устройство «ничего не знает» о номере «помеченного» провода. Мы назовем это устройство — диффузионный оператор, и он будет изменять состояния электрона по следующему правилу:
Присмотритесь, в отличие от Оракула, у этого оператора нет «любимчиков», все провода равноправны.
Итак, алгоритм Гровера для поиска помеченного элемента в базе данных из четырех элементов:
1) Равномерно «размазать» электрон по всем четырём проводам
2) Пропустить такой размазанный электрон через Оракул, получив на выходе (мы ранее условились, что помеченный провод — это третий)
3) Пропустить уже этот электрон через диффузионный оператор, на выходе из которого получить
4) Измерить на каком проводе сидит электрон. Всё.
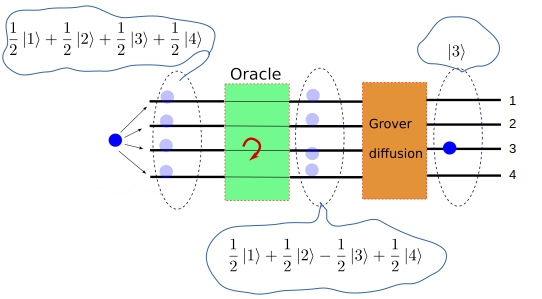
Итак, нам оказалось нужно всего одно обращение к Оракулу! А если бы мы искали классическим способом, то нам было бы нужно в среднем обратиться к Оракулу два с половиной раза. Как это посчитать? Очень просто: в 1/4 случаев мы бы угадали с первого раза, в 1/4 случаев угадали бы со второго раза… а в среднем, число обращений к Оракулу было бы равно
Если же у нас N не четыре, а, скажем, миллион, то алгоритм выглядит точно так же: распределяем один электрон равномерно по миллиону проводов, пропускаем через Оракул, затем через диффузионный оператор, затем опять через Оракул, а потом опять через диффузионный оператор,.. и так примерно тысячу раз, после чего электрон будет сосредоточен на нужном проводе, номер которого мы ищем и номер которого «знает»Оракул. Вдумчивый читатель может спросить: а где же в алгоритме Гровера кубиты? Ответ такой: все эти разговоры про «электрон, размазанный по проводам» можно перевести на язык кубитов и операций над ними. Как именно это делается — можно увидеть на сайте квантового компьютера IBM-Q, ссылку на который я давал выше.
Пара слов о том, что такое квантовый компьютер D-Wave, в котором уже есть тысячи кубитов. Это не универсальный квантовый компьютер, и он работает не так, как я описывал выше. Компьютер D-Wave можно называть «устройство квантового отжига», и он эффективен для задач оптимизации. Что такое оптимизация? Это похоже на задачу поиска. Представьте себе абстрактный (но в меру абстрактный) ландшафт: холмы, ямы и овраги. И нужно найти самую глубокую яму. Классическое решение: берётся мячик и его случайно бросают на ландшафт. Мячик как-то катится вниз, пока не попадает в какую-то яму. Но это может быть не та яма, которую мы ищем, не самая глубокая. Чтобы выбраться из этой ямы и продолжить поиски, мячику нужно прыгнуть. А вероятность того, что в течение следующих секунд мячик прыгнет и интенсивность прыжка определяется температурой. Чем выше температура, тем интенсивнее прыгает мячик и тем легче выбирается из ям. Но мы медленно понижаем температуру так, что если мячик уже попал в самую глубокую яму, то ему уже не хватит температуры, чтобы выпрыгнуть, но если яма не самая глубокая, то температуры пока ещёхватает, чтобы выпрыгнуть и попытать счастья в другом месте. И в принципе, когда мы понижаем температуру медленно, то шанс в конце увидеть мячик именно в той яме которую мы ищем — ну.. есть в общем шанс. Но мячик может, конечно, застрять в неправильной, не самой глубокой яме. Это суть и проблемы классического отжига.

Квантовый отжиг, который использует D-Wave можно представить себе так. Давайте сначала организуем очень простой ландшафт. В этом «искусственном» ландшафте тоже есть ямы разной глубины и холмы, но мы все координаты ям и их глубины знаем заранее, и мы сами помещаем мячик в самую глубокую яму. А теперь, когда мячик уже в самой глубокой яме, мы не понижаем температуру как это было в классическом отжиге (температура и так очень низкая), а медленно и без скачков изменяем ландшафт к той сложной форме, которая нам интересна. И благодаря тому, что мячик, лежащий в самой глубокой яме — это квантовый мячик, а также благодаря адиабатической теореме, которая была доказана в 1928 году, нам гарантируется, что мячик будет оставаться в самой глубокой яме всёто время, пока медленно меняется ландшафт. То есть, глубина и местоположение самой глубокой ямы с изменением ландшафта меняются, но тот факт, что мячик находится именно в самой глубокой яме на текущий момент — неизменен. И в конце трансформации ландшафта мы получим таки мячик в самой глубокой яме интересующего нас ландшафта. Программирование и контроль ландшафтов в компьютере D-Wave происходит с помощью настройки того, как каждый кубит взаимодействует с другими кубитами. Например, тот «искусственный» вспомогательный ландшафт, с которого стартуют, соответствует простой ситуации, когда все кубиты «не видят» друг друга. А потом медленно включают запрограммированное взаимодействие, причёмвсех со всеми сразу, а не попарно по очереди, как было описано ранее.
Проблемы и хейтеры. Когда я писал о том, что вот, дескать, лежат себе кубиты, а мы по очереди их спариваем друг с другом и крутим, то это было упрощение. На самом деле, кубиты постоянно «чувствуют» своёокружение (то, на чём они, собственно, «лежат») и взаимодействуют с ним. Из-за этого неконтролируемого процесса возникают ошибки. Как с ними пытаются бороться — это отдельная большая тема. Некоторые ученые считают, что построить квантовый компьютер вообще невозможно и вся эта деятельность — только лишь проедание государственных средств. Одним из известных последовательных критиков идеи построения квантового компьютера является Михаил Дьяконов (Michel Dyakonov), статьи и язвительные презентации которого можно найти в интернете.
Получится ли построить универсальный квантовый компьютер или нет —я не знаю. Но по крайней мере попытка была интересной и дала повод человечеству подумать о том, какие вычислительные ресурсы стоят за квантово-механическим поведением в природе. Дэвид Дойч, которого я тут упоминал, считает, что уже сама теоретическая возможность создания квантового компьютера свидетельствует в пользу реальности параллельных вселенных, о которых заявлял Хью Эверетт.
Прошу прощения зу читателей за возможные ляпы и неточности.
Литература:
- Майкл А. Нильсен, Исаак Л. Чанг, "Квантовые вычисления и квантовая информация"
- Иванов М. Г., "Как понимать квантовую механику"
Блог и twitter автора: http://rotozeev.net, @rotozeev